こんにちは!バックエンドエンジニアのjunyaUと申します。
最近はコンビニに売っている生ラムネにハマっていて、1日2袋のペースで食べ続けていましたが、ここ数日コンビニに置いていなくて悲しい思いをしています。
今回は配列と連結リストおいて、線形探索の計算速度はどちらが速いのか、キャッシュメモリがどう関わっているのかについて考えていこうと思います〜!
はじめに
なぜ記事を書こうと思ったのか
最近、個人開発で物理メモリ管理の実装をする機会がありました。
その中で、配列を線形探索する処理があったのですが、
「連結リストと配列を線形探索する時に、どちらの方が計算速度が速いんだろう」
とふと疑問に思ったのがきっかけです。
この問題を調べて勉強していくうちに、キャッシュメモリの存在が両者の計算速度の違いに関わっていることがわかりました。
そこで、配列と連結リストのデータ構造の違い、キャッシュメモリがどのようなものなのかについて触れながら両者の線形探索における計算速度の違いを見ていこうと思います!
なお、ここでの連結リストは単方向の連結リストとします。
結論
配列と連結リストは共に線形探索の時間計算量がO(n)ですが、計算速度は配列の方が速いです。
これは、キャッシュメモリのヒット率が配列の方が高いからです。
連結リストはメモリ上で非連続的に配置される可能性がありますが、配列はメモリ上に連続で配置されることが保証されています。
連続してメモリ上に配置されているので、キャッシュラインに配列の他の要素が含まれる可能性が高いため、キャッシュヒット率が連結リストよりも高くなるのです。
これを理解するには配列と連結リストの構造の違い、キャッシュメモリの概要や特性を知る必要があるので、次節から詳しく見ていきたいと思います。
配列と連結リスト
配列の特徴
私がプログラミングを勉強し始めた頃、配列は「複数のデータを入れることができる箱」と学びました。
しかしそれだけでは、配列がどのような実態を持っているのかを掴めないので、もう少し具体的に定義すると、
「メモリ上に連続して配置された、同じ種類のデータの集合」と言えます。
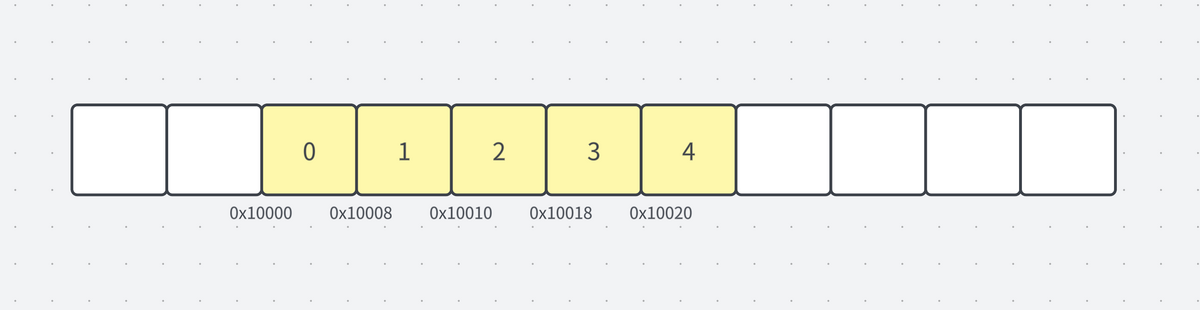
メモリに連続して配置されているので、要素のサイズ分アドレスがずれて要素が配置されていることがわかるかと思います。
連続して配置することによって、いくつかの特性や利点が生まれます。
ランダムアクセス可能
ランダムアクセスは、インデックスを用いて任意の要素に直接アクセスする操作を指します。
例えば、array[2]のような操作と考えれば馴染み深いと思います。
このような直接アクセスが可能なのは、配列の要素がメモリ上に連続して配置されているためです。
アクセスのメカニズムは単純で、arrayという変数には配列の先頭アドレスが格納されており、このアドレスに「要素のサイズ × インデックス」を加えることで、目的の要素のアドレスを瞬時に計算することができます。
array[3] というアクセスがあった場合:
0x10000 + (8 × 3) = 0x10018
この計算でアドレスを求めることによって、O(1)の時間計算量で該当の要素にアクセスすることができます。
配列のインデックスが0から始まる理由も、このメモリ上の連続した配置と密接に関連しています。「なぜ0から?」と初めは誰もが疑問に感じると思いますが、メモリの観点から考えると、アドレス計算を効率化するためであることが明白になります。
削除と挿入操作時のオーバーヘッドが大きい
配列の末尾に対して、挿入や削除をする場合の時間計算量はO(1)です。
しかし先頭や中間に挿入や削除を行う場合、追加の時間計算量がかかります。
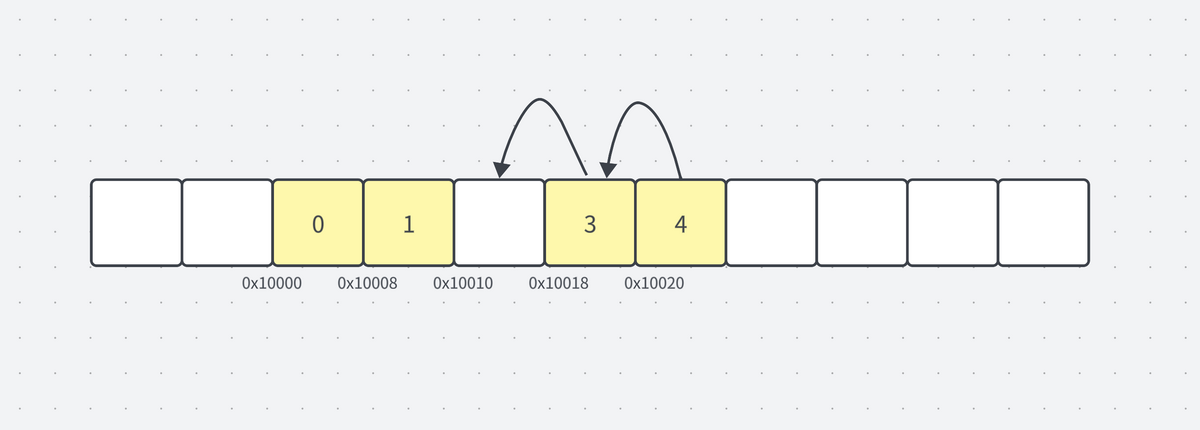
削除すると、その位置に空きが生まれます。この空きを埋めるために、削除した要素以降の要素を全て1つ前にずらす必要が出てきます。この操作は、特に配列が大きい場合、大きなオーバーヘッドが発生します。
今回のケースではindex3とindex4の要素を1つ前にずらすという操作が必要となります。
このようなオーバーヘッドを考慮すると、頻繁に削除や挿入が行われるケースでは、配列を使うのではなく、他のデータ構造を使うべきだと言えます。
固定長
C, C++, Java, および Go などの配列は固定長であり、一度確保したサイズを途中で変更することはできません。主な理由は、配列が連続したメモリ領域に配置されているためです。
拡張をしようとしても、配列の直後のメモリには別のデータが配置されている可能性があります。
また、仮に配列を後に拡張するために余分にメモリを確保するとしても、それが後で使用されるかどうか予測することが難しく、メモリの浪費につながります。
なので、データ長を動的に変えたい場合、配列は適したデータ構造ではありません。
連結リストの特徴
連結リストは、複数のデータを管理するという観点では配列と同じですが、そのデータ構造は全く違います。
配列はデータを連続したメモリ領域に確保しますが、連結リストはそのような連続性を保証しません。
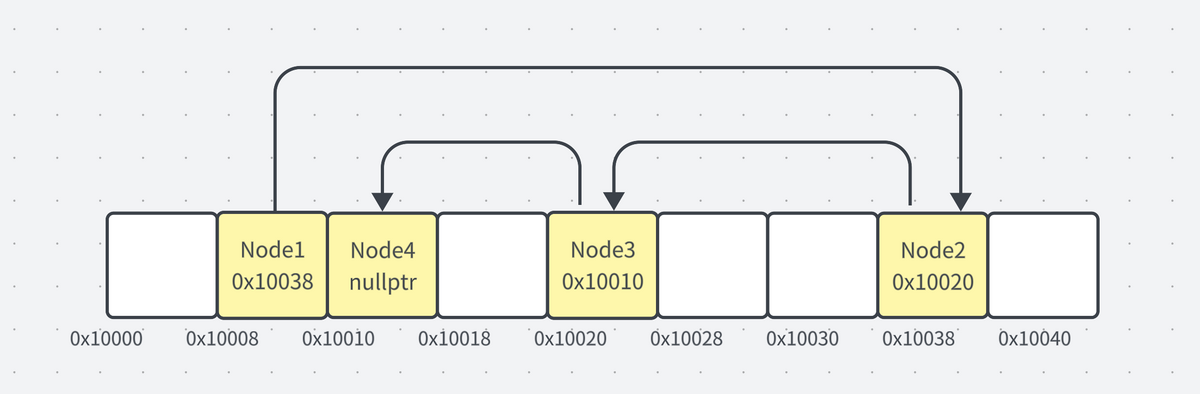
連結リストの各要素(ノードとも呼ばれる)はデータと、次の要素への参照(ポインタ)を持っています。このポインタをたどることで、次の要素にアクセスすることができ、非連続でも複数データを管理することができます。
このように非連続で配置することによって、いくつかの特性や利点が生まれます。
ランダムアクセスはできない
連結リストは、特定の要素への直接アクセスが配列と比べると非効率です。
配列ではarray[3]のように特定のインデックスを指定して、O(1)の時間計算量でその要素にアクセスできます。
一方、連結リストではデータが連続したメモリ領域に格納されていないため、ベースアドレスを使用してインデックス計算で要素のアドレスを直接特定(ランダムアクセス)することはできません。
n番目の要素にアクセスするためには、連結リストの先頭から、指定された位置に達するまで各要素のポインタを逐次たどる必要があります。
この操作はO(n)の時間計算量がかかることになります。
そのため、特定の要素への高速なアクセスが必要な場合は、連結リストよりも配列を使用する方が適切です。
削除と挿入時のオーバーヘッドが小さい
配列では先頭や中間への要素の挿入や削除に大きなオーバーヘッドがかかりますが、連結リストではこれらの操作をより小さいオーバーヘッドで行うことができます。
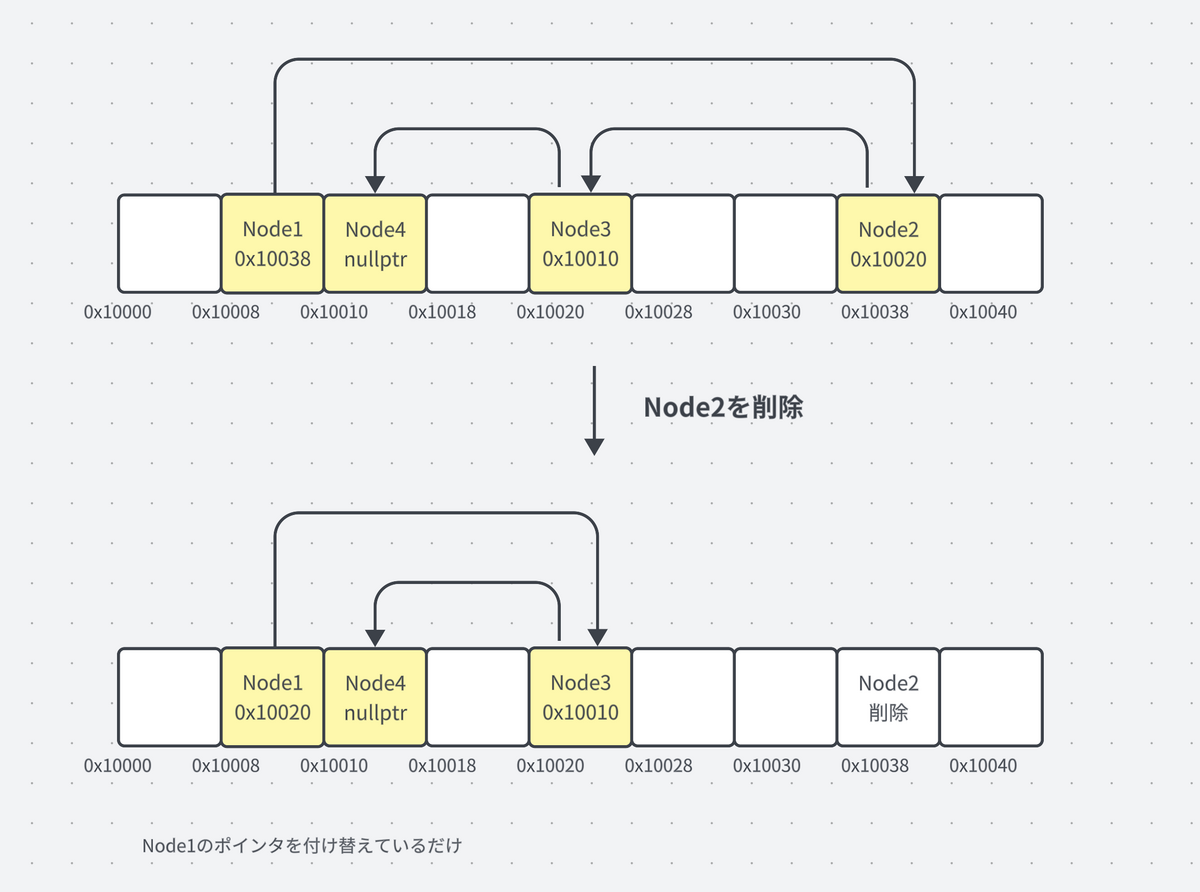
Node1が持っていたNode2へのポインタをNode3へのポインタに付け替えるだけで削除の操作は完了します。
このように、頻繁に削除や挿入が行われるケースは配列よりも連結リストの方が適しています。
可変長
連結リストは可変長のデータ構造です。
配列と違い、データを連続して配置する必要はないので、拡張が必要な場合は都度空いているメモリにNodeを割り当て、連結リストを拡張することができます。
動的なデータ長を扱う場合、配列よりも連結リストの方が適したデータ構造と言えます。
比較表
最後にそれぞれの特徴をまとめた表を置いておきます。
| 特徴/操作 | 配列 | 連結リスト |
|---|---|---|
| メモリの配置 | 連続 | 非連続 |
| ランダムアクセス | O(1)(高速) | O(n)(低速) |
| 先頭や中間への要素の挿入・削除 | O(n)(低速、要素をずらす必要がある) | O(1)(高速、ポインタを更新するだけ) |
| メモリ使用効率 | 低い(固定長) | 高い(可変長) |
| サイズ変更 | 困難/不可能(再確保とコピーが必要) | 容易(要素の追加・削除でサイズ変更) |
線形探索
線形探索について
今回の主題である、連結リストと配列において線形探索する時に、どちらの方が計算コストが少ないのかという問題を考える前に、線形探索について軽く触れておこうと思います。
線型探索は検索のアルゴリズムの1つで、 連結リストや配列に入ったデータに対する検索を行うにあたって、 先頭から順に比較を行いそれが見つかれば終了するといったアルゴリズムです。
優秀なアルゴリズムですが、先頭から片っ端に探していくので「馬鹿サーチ」とも呼ばれているみたいです。(ひどい…😭)
ちなみに連結リストの節で
n番目の要素にアクセスするためには、連結リストの先頭から、指定された位置に達するまで各要素のポインタを逐次たどる必要があります。
このように、ランダムアクセスではなく先頭から逐次辿る必要があると述べましたが、まさにこれが線形探索となります。
どちらの方が計算コストが低いのか
線形探索自体の時間計算量はO(n)となりますが、実際の実行速度はデータ構造によって異なります。
配列と連結リストでは、どちらの方が速く探索できるのかを、実際にコードを書いて検証してみます。
なお今回はC++を使うことにします。
#include <iostream> #include <forward_list> #include <random> #include <algorithm> #include <chrono> #include <vector> #include <numeric> #include <cmath> // Generate random data for testing template<typename Container> void generate_data(Container &c, size_t size) { std::random_device rd; std::mt19937 mt(rd()); std::uniform_int_distribution<int> dist(1, 1000000); c.resize(size); std::generate(c.begin(), c.end(), [&mt, &dist]() { return dist(mt); }); } template<typename Container> void linear_search_test(const Container &c, const std::string &type) { const int repeat_count = 200; std::vector<long long> times; for (int i = 0; i < repeat_count; ++i) { auto start = std::chrono::system_clock::now(); // Perform a dummy operation to prevent loop optimization int sum = 0; for (const auto &val: c) { sum += val; } auto end = std::chrono::system_clock::now(); auto elapsed = std::chrono::duration_cast<std::chrono::microseconds>(end - start); times.push_back(elapsed.count()); } double mean_time = std::accumulate(times.begin(), times.end(), 0.0) / repeat_count; double sq_sum = std::inner_product(times.begin(), times.end(), times.begin(), 0.0); double stdev_time = std::sqrt(sq_sum / repeat_count - mean_time * mean_time); double cv = stdev_time / mean_time * 100; std::cout << "Type: " << type << "\n"; std::cout << "Average time: " << mean_time << "μs\n"; std::cout << "Time stddev: " << stdev_time << "μs\n"; std::cout << "Coefficient of variation: " << cv << "%\n\n"; } int main() { const size_t data_size = 10000000; std::vector<int> vec; std::forward_list<int> list(data_size); generate_data(vec, data_size); generate_data(list, data_size); linear_search_test(vec, "Vector"); linear_search_test(list, "Forward List"); return 0; }
これは、1000万個の要素を持つ連結リストと配列に対して、線形探索を200回ずつ行いそれぞれにかかった時間を計測するコードです。
結果の前に、計測するにあたって考慮した点を軽く紹介していこうと思います。
配列はarrayではなくvectorを使う
今回は、配列の表現に、std::arrayではなくstd::vectorを使うようにしました。
これは、連結リストと同じメモリ領域を使うためです。
std::arrayとstd::vectorはどちらも配列を表すデータ構造ですが、使われるメモリ領域が異なります。
std::arrayはコンパイル時にサイズが確定するのでスタック領域に割り当てられますが、
std::vectorはヒープ領域に割り当てられます。
それぞれのメモリ領域に軽く触れておくと :
- スタック領域は、通常は関数の呼び出しや局所変数の保存に利用されるメモリ領域で、アクセス速度が速い
- ヒープ領域は、動的にデータを割り当てる際に使用されるメモリ領域で、メモリアクセスの速度はスタックに比べて遅い
となっています。
この検証では、「メモリ領域の違い」ではなく「メモリの連続性」に焦点を当てています。
なので、配列と連結リストで使用するメモリ領域を揃えることで、メモリの連続性による影響を強調できるようにしました。
コンパイラがループを最適化しないようにした
線形探索に該当するループの部分でsumという変数に加算を行っています。
これは、何もループ内に処理を書かなければ、この部分の実行はする必要がないとコンパイラに判断されその部分は省略(最適化)されてしまうため、最適化されないようにダミーの処理を追加しています。
結果
こちらが検証に使用したマシンのスペックです。
- CPU: Apple M2 Max
- RAM: 64GB
- OS: Ventura 13.4
このマシンでそれぞれ200回実行した結果は次のようになりました。
Type: Vector Average time: 47886.5μs Time stddev: 1139.39μs Coefficient of variation: 2.3794% Type: Forward List Average time: 60295.2μs Time stddev: 1518.22μs Coefficient of variation: 2.5180%
結果から明らかなのは、配列(Vector)と連結リスト(Forward List)の平均実行時間には約12,000マイクロ秒の差があるという点です。また、両方のデータ構造における係数の変動(Coefficient of Variation)が低いことから、このデータは一定の信頼性を持っていると判断できます。
(マシンやリソースの状況によって結果は異なりますが)
では、なぜ時間計算量が両方ともO(n)であるにも関わらず、このような実行時間の差が生まれるのでしょうか?
これは、データのメモリ配置に関わる「キャッシュ効率」が大きな要因の1つとして挙げられます。
連続したメモリ領域に配置された配列は、キャッシュメモリにおいて高いヒット率を示すため、全体として計算コストが削減されるのです。
なぜ配列の方がヒット率が高くなるのでしょうか?
ここで登場したキャッシュメモリが持つこれらの性質と、なぜヒット率が異なるのかを次の章で詳しく見ていきます。
キャッシュメモリ
キャッシュメモリの概要
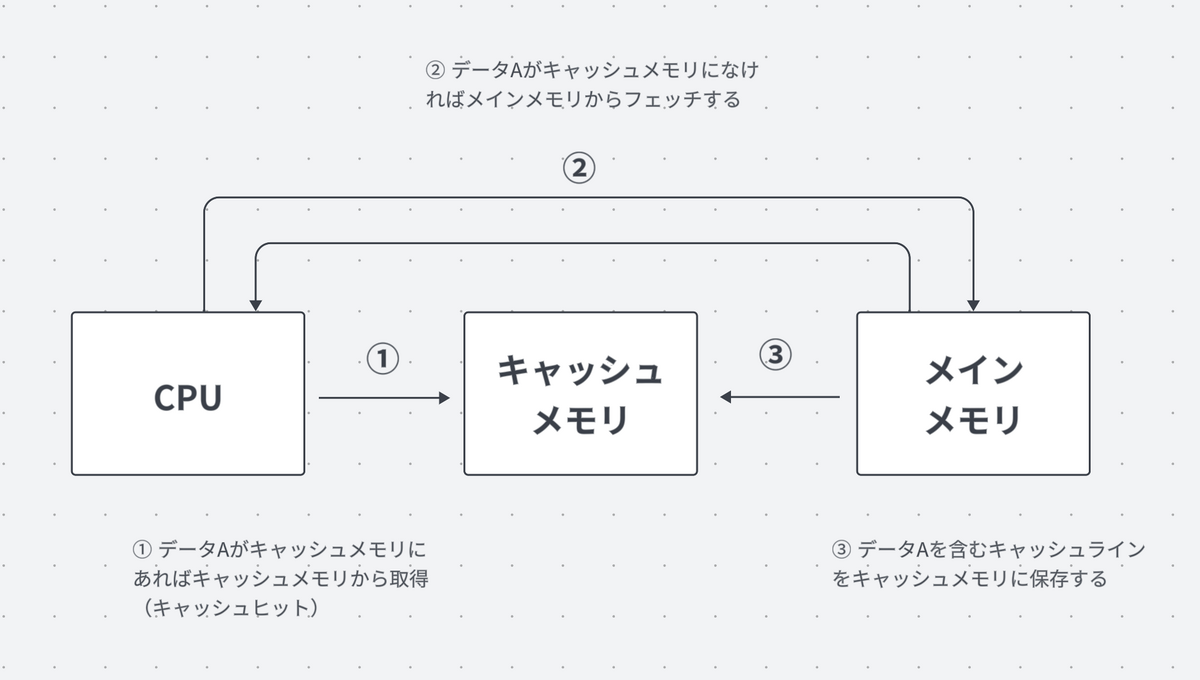
キャッシュメモリは、CPU(処理装置)とメインメモリ(主記憶装置)の中間に位置する、高速なデータアクセスが可能な小さな記憶装置です。
ノイマン型アーキテクチャのコンピュータでは、CPUとメインメモリの処理性能には性能差があります。
いくらCPUの性能を高めようと、そのCPUの処理性能にメインメモリのアクセス速度が追いつけません。 そのため、メインメモリからデータをフェッチする速度の遅さがボトルネックとなり、システム全体の処理速度も遅くなります。
この現象は「ノイマンボトルネック」と呼ばれています。
キャッシュメモリは、両者の処理性能差を埋め合わせることでこの問題の解決を図ります。
具体的には、処理装置がアクセスしたデータやアドレスなどをキャッシュメモリに一時的に保持しておくことで、次に同じデータやアドレスにアクセスがあった場合、メインメモリではなくキャッシュメモリから迅速にデータをフェッチできます。
これにより、メインメモリへのアクセスが削減され、データフェッチの効率の向上、高速化が見込めます。
キャッシュメモリはL1,L2,L3といった複数のレベルを持っています。
記憶階層において、このレベルの数字が小さいほどCPUに近く高速になります。
補足 : 記憶階層とは?
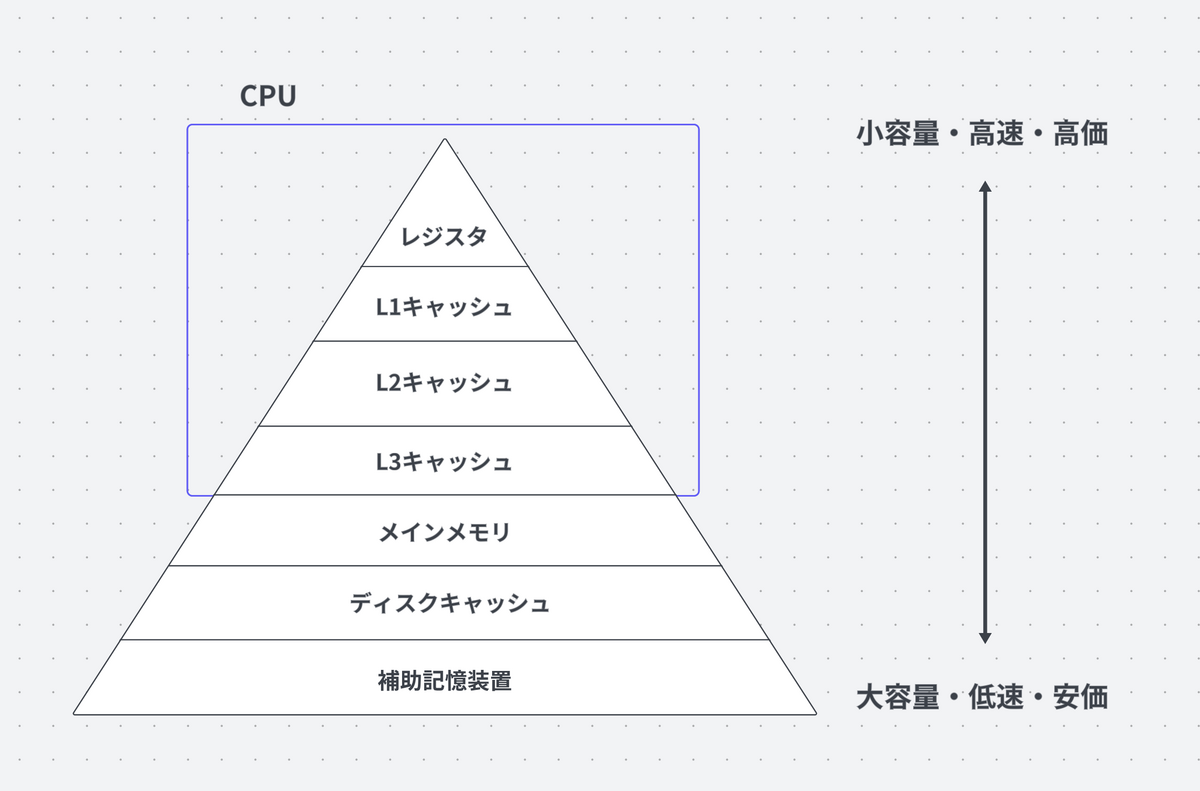
CPUにとって、望ましい記憶装置は大容量で高速にアクセスできるものです。
しかし、実際の記憶装置は大容量であるほどアクセス速度が遅くなり、小容量であるほど高速になるというトレードオフがあるので、望むような記憶装置は現状作ることができません。
そこで図のように記憶装置を階層化し、各階層を下位の階層のキャッシュとして用いることで、CPUから見た場合、あたかも大容量で高速な1つの記憶装置であるかのように振舞います。
このように階層化された記憶システムを、記憶階層と言います。
なぜ配列の方がヒット率が高いのか
配列が連結リストと比べてキャッシュメモリのヒット率が高くなる理由は、その連続したメモリ構造とキャッシュメモリのデータ取得方法に密接な関連があります。
キャッシュメモリは「キャッシュライン」という一定の単位でデータを一時的に保持しています。
キャッシュラインのサイズは、プロセッサのアーキテクチャやモデルによって異なりますが、32、64、または128バイトが一般的です。
メインメモリからデータAをフェッチする際、キャッシュメモリはデータAだけでなく、その近傍のデータも合わせて保持します。したがって、次に近傍のデータにアクセスする際はヒットする確率が高くなります。
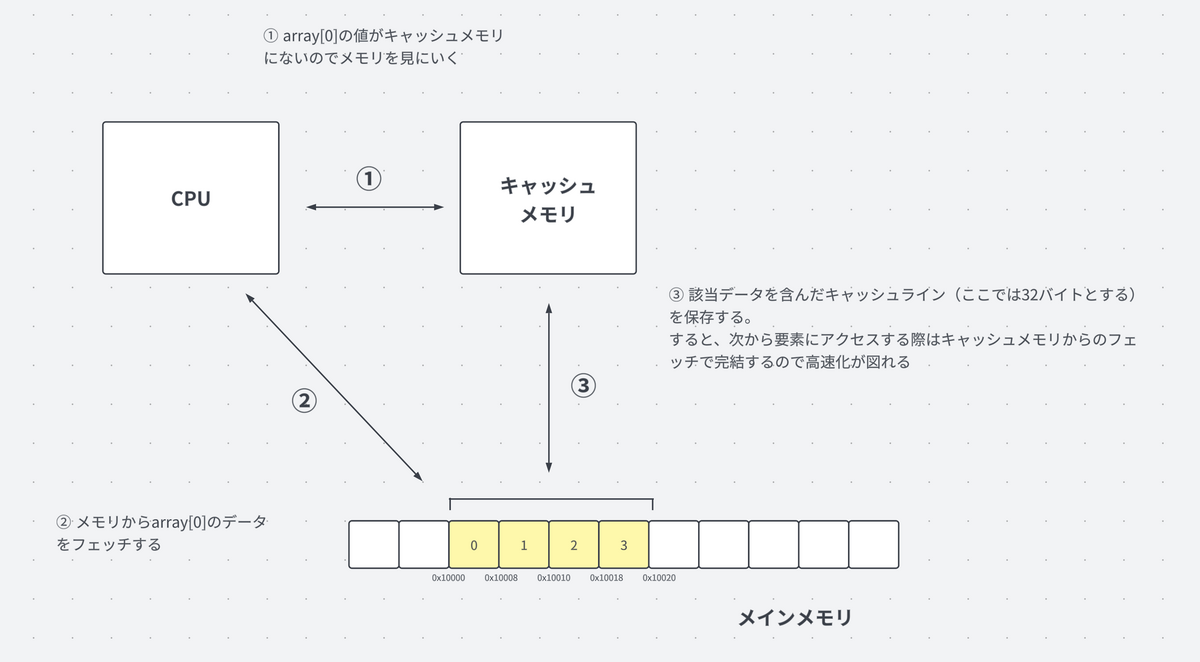
例として、上図のarray[0]の要素をフェッチする場合を考えてみます。
array[0]をメモリからフェッチする際、その近傍のデータもキャッシュライン(ここでは例として32バイト)としてキャッシュメモリに一時保存します。
すると、4つ全ての要素がキャッシュメモリに保持され、次にこれらの要素にアクセスする際は、メインメモリよりも高速なキャッシュメモリからデータをフェッチすることができます。
これは、配列のメモリ上での連続した配置と、キャッシュメモリがキャッシュライン単位で近傍のデータも一緒に保存する性質とが組み合わさって実現されます。
一方で、連結リストではメモリ上に非連続に配置されているため、キャッシュミスが配列に比べて頻発します。
これが、配列と連結リストの間でキャッシュヒット率が異なる理由です。
また、このキャッシュラインによる近傍データの同時フェッチの考え方は、「空間的局所性」というコンピューティングの性質に基づいています。
空間的局所性
空間的局所性は、一度アクセスされたデータの近傍が近いうちに再びアクセスされる可能性が高い、というプログラムの実行特性を指します。
キャッシュメモリの設計において、キャッシュラインがこの特性に基づいています。
具体的には、一度データをフェッチすると、その近くにあるデータも一緒にキャッシュに取り込むことで、次のアクセスが高速になる可能性が高くなります。
時間的局所性
時間的局所性は本例では触れられていませんが、こちらも重要な特性ですので補足として紹介しておきます。
時間的局所性とは、一度アクセスされたデータが近いうちに再度アクセスされる可能性が高いという特性を指します。
webブラウザにおいて、「戻る」ボタンを押す行動もこの一例となります。
ブラウザは、この操作を高速に行うため、以前アクセスしたページのデータをキャッシュしており、これは時間的局所性に基づいたものになります。
おわりに
結論
配列が連結リストと比較して、線形探索の際のメモリアクセスのコストが低いことがわかりました。
この違いは、配列のほうがキャッシュメモリに対して高いヒット率を示すためです。
キャッシュメモリが高いヒット率を持つ背後には、キャッシュメモリが「空間的局所性」の原理に基づいて設計されていること、及び配列のデータがメモリ上で連続して配置される特性があります。
具体的には、キャッシュメモリはキャッシュラインと呼ばれる単位で近傍のデータも一緒に保持し、これによって近くのデータにアクセスする際もキャッシュから高速にデータを取得することができるので、結果的に配列の線形探索の方が早くなったのでした。
このようにハードウェアの特性や概念を知ることで、コンピュータリソースをより効率的に扱えるようになることにつながります。
Web開発においては、「業務で使わないから」という理由で低レイヤーやアルゴリズムの勉強が軽視されることがありますが、こういった抽象化されている部分を勉強することは、
普段使っている技術への理解が深まりスキルの向上につながると思うので、引き続きこういった内容のブログを発信していこうと思っています!
また、キャッシュメモリは他にもデータの一貫性を保つための「キャッシュコヒーレンシ」など、面白い仕組みがまだまだあるので、機会があればこちらもまた書いていこうと思います〜!